
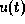 und des zugehörigen
optimalen Zustands- und Geschwindigkeitsverlaufes
und des zugehörigen
optimalen Zustands- und Geschwindigkeitsverlaufes 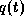 ,
,  ist ein geeignetes Funktional
ist ein geeignetes Funktional 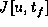 hinsichtlich der Steuervariablen u und der ggf. freien Verfahrzeit
hinsichtlich der Steuervariablen u und der ggf. freien Verfahrzeit  zu minimieren (optimale Steuerung).
Dabei sind die dynamischen
Gleichungen (1), evtl. vorgeschriebene
Anfangs- und Endbedingungen (
zu minimieren (optimale Steuerung).
Dabei sind die dynamischen
Gleichungen (1), evtl. vorgeschriebene
Anfangs- und Endbedingungen ( ,
, 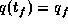 , etc.)
sowie weitere Beschränkungen der Form
, etc.)
sowie weitere Beschränkungen der Form 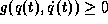 einzuhalten.
einzuhalten.
Unterschiedliche Aufgaben erfordern unterschiedliche Gütekriterien J für optimale Bahnen. Wenn, wie bei Punktschweiß- oder Handlingsaufgaben, nur Anfangs- und Endstellung der Bewegung vorgegeben sind, sind typischerweise zeitoptimale Punkt-zu-Punkt Bahnen gesucht

Bei Klebevorgängen ist es andererseits erforderlich, während der gesamten Bewegung eine vorgeschriebene Bahn optimal abzufahren.
Selbst für komplizierteste Robotermodelle kann leicht mit den Mitteln der Optimalsteuerungstheorie nachgewiesen werden, daß bei zeitminimaler Steuerung immer mindestens ein Motor an seinem Limit operieren muß. Andererseits zeigen die numerischen Ergebnisse, daß zeitminimale Punkt-zu-Punkt Bewegungen meist eine unerwartete Schaltstruktur mit vielen Umschaltungen zwischen maximalen Antriebs- und Bremsmomenten besitzen (sogenannte bang-bang Steuerungen) und dabei enorme Belastungen auf die Gelenke ausüben. Hier bieten schnelle, energieminimierende Bewegungskriterien wie
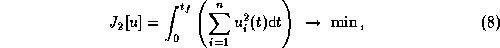
die bei geeignet vorgeschriebener Endzeit  nur wenig langsamere
Bewegungen als die zeitminimale liefern, einen guten Kompromiß
zwischen Verfahrzeit und Verschleiß [vS], [vSSch].
Die vorab berechnete theoretisch schnellstmögliche Verfahrzeit
dient dabei als Schranke in der Berechnung einer z.B. 20% langsameren,
energieminimalen Bewegung.
nur wenig langsamere
Bewegungen als die zeitminimale liefern, einen guten Kompromiß
zwischen Verfahrzeit und Verschleiß [vS], [vSSch].
Die vorab berechnete theoretisch schnellstmögliche Verfahrzeit
dient dabei als Schranke in der Berechnung einer z.B. 20% langsameren,
energieminimalen Bewegung.
Das Bahnoptimierungsverfahren muß eine problemlose Optimierung für komplexe Roboterdynamiken, sowie sehr unterschiedliche Gütekriterien und Beschränkungen ermöglichen. Hierzu wurde ein sogenanntes direktes Kollokationsverfahren entwickelt und implementiert [vS]. Die Methode beruht auf einer Diskretisierung der Zustandsvariablen durch stückweise kubische Splinefunktionen, die die Differentialgleichungen an den Gitterpunkten der Diskretisierung und den dazwischen liegenden Mittelpunkten erfüllen (Kollokation). Die Steuerungen werden durch stückweise lineare Funktionen approximiert. Durch diese Diskretisierung wird das optimale Steuerungsproblem in ein endlich-dimensionales nichtlineares beschränktes Optimierungsproblem übergeführt, welches mit SQP-Verfahren gelöst werden kann [GiMuSaWr]. Durch diesen direkten Lösungsansatz kann eine optimale Steuerung näherungsweise berechnet werden, ohne mit den oft schwierigen notwendigen Bedingungen der Optimalsteuerungstheorie (adjungierte Differentialgleichungen etc.) umgehen zu müssen (indirekter Ansatz).
Verglichen mit anderen numerischen Methoden der optimalen Steuerung ist dieses direkte Kollokationsverfahren relativ einfach zu verwenden (da Kenntnisse der Theorie optimaler Steuerungen nicht notwendigerweise zur Bedienung erforderlich sind), robust (da sehr wenig Information über die Lösung a priori benötigt wird) und zuverlässig (da die erreichbaren Genauigkeiten für die Roboterbahnoptimierung völlig ausreichend sind) [vS].
Während die beschriebene Kollokationsmethode allgemein zur
numerischen Lösung optimaler Steuerungsprobleme eingesetzt werden
kann, wurde im Projekt eine weitere Diskretisierung entwickelt
und implementiert, die zusätzlich die spezielle Struktur der Roboterdynamik
(1) (Mehrkörpersystem in Minimalkoordinaten)
ausnützt. Dabei wird die Transformation des semi-impliziten
Systems von n Differentialgleichungen zweiter Ordnung (1)
auf die Standardform eines Systems erster Ordnung
mit 2n Differentialgleichungen (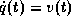 ,
, 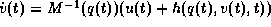 vermieden.
Im Vergleich zu Standardverfahren führt die neue Diskretisierung
zu sehr viel kleineren nichtlinearen
Optimierungsproblemen. In zusätzlicher Kombination mit
Sparse-Optimierungsmethoden können die Berechnungszeiten so
um einen Faktor im Bereich von 10 bis 20 verkürzt werden
[OlvS].
Die optimale Bahnplanung ist damit im Bereich von etwa einer Minute
auf Standardrechnern (PCs oder Workstations) durchführbar
geworden.
vermieden.
Im Vergleich zu Standardverfahren führt die neue Diskretisierung
zu sehr viel kleineren nichtlinearen
Optimierungsproblemen. In zusätzlicher Kombination mit
Sparse-Optimierungsmethoden können die Berechnungszeiten so
um einen Faktor im Bereich von 10 bis 20 verkürzt werden
[OlvS].
Die optimale Bahnplanung ist damit im Bereich von etwa einer Minute
auf Standardrechnern (PCs oder Workstations) durchführbar
geworden.
Beispiel: Schnelle Punkt-zu-Punkt Bahnen von A nach B werden für einen Roboter vom Typ Manutec r3 [OtTü] in drei Freiheitsgraden (n=3) und bei einer Last von 0kg untersucht:
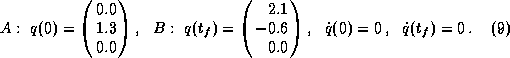
Achtzehn technische Beschränkungen
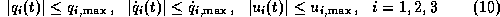
müssen bei der Planung optimaler Bahnen berücksichtigt werden [OtTü], [vS], [vSSch].
Die berechnete zeitoptimale Bahn mit  s
ist in Abb.5 dargestellt.
Danach wird die verbrauchsminimale Bahn (vgl. [PfRe])
s
ist in Abb.5 dargestellt.
Danach wird die verbrauchsminimale Bahn (vgl. [PfRe])

für eine feste, vorgeschriebene Endzeit von  s
berechnet, welche 21% langsamer ist
(Abb.6).
Das minimale Integralkriterium ist
s
berechnet, welche 21% langsamer ist
(Abb.6).
Das minimale Integralkriterium ist  .
Der entsprechende Wert für die zeitminimale Bewegung liegt bei
.
Der entsprechende Wert für die zeitminimale Bewegung liegt bei  .
.
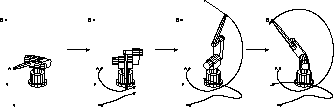
Figure 5: Zeitminimale Bewegung von A nach B in 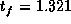 s.
s.
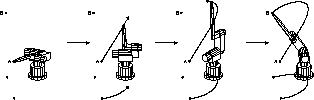
Figure 6: Verbrauchsminimale Bewegung von A nach B in 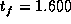 s.
s.