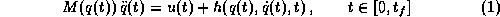
Die mathematische Beschreibung (Modellierung) erfordert zunächst die geometrische Beschreibung des konkreten Roboters in seiner Arbeitszelle. Das kinematische Robotermodell beschreibt die Robotergeometrie in einer parametrischen Form, die zur Positionierung des Endeffektors verwendet wird. Da die Roboterbewegungen sehr schnell sind, müssen bei der Bahnoptimierung auch Massenverteilungen, Trägheitsmomente, sowie Zentrifugal-, Coriolis-, Gravitations- und Reibungskräfte berücksichtigt werden. Als Mehrkörpersystem in Minimalkoordinaten wird das dynamische Verhalten durch ein System von n Differentialgleichungen in den Gelenkkoordinaten beschrieben (n ist die Anzahl der rotatorischen und translatorischen Robotergelenke):
bzw. für n=3
Die Gelenkkoordinaten
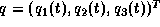sind die Zustandsvariablen, und
die normalisierten Momentensteuerungen 
sind die Steuervariablen.
Die Matrix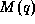 
von Trägheitsmomenten ist positiv definit und symmetrisch.
Die durch Coriolis-, Zentrifugal-,
Gravitations- und Reibungskräfte bedingten Momente
sind in 
enthalten.
Zur rechnergestützten Formulierung der Differentialgleichungen
stehen effiziente Mehrkörperalgorithmen
zur Verfügung [Schi].
Außer technischen Beschränkungen, wie den maximalen Motorspannungen, maximalen Gelenkwinkelgeschwindigkeiten und maximalen Koordinatenverläufen, sind geometrische Beschränkungen zur Kollisionsvermeidung mit der Arbeitszelle oder anderen Objekten im Arbeitsbereich des Roboters bei der Berechnung optimaler Bewegungen unbedingt zu berücksichtigen. Im Rahmen des Projektes wurde hierzu eine besonders effiziente Methode zur Modellierung der Kollisionsvermeidung entwickelt [Sta].
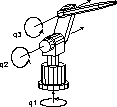
Figure 3: Robotermodell mit n=3 Freiheitsgraden (rotatorische Gelenke).
