


Next: Bahnoptimierung
Up: Beschreibung der zu
Previous: Modellierung
Um das reale kinematische oder dynamische Verhalten eines konkreten
Roboters hinreichend genau beschreiben zu können, müssen
Parameter wie
geometrische und kinematische Grössen, Massen der Teilkörper,
Trägheitsparameter, Reibungskoeffizienten u.a. bekannt sein.
Unterschiedliche Methoden zur Roboterkalibrierung
durch direkte oder indirekte Vermessung sind verfügbar,
um die Genauigkeit kinematischer Modelle
zu verbessern [BeAl].
Bei der indirekten Vermessung werden die kinematischen Parameter
durch Vergleich von Soll- und Ist-Bahnen berechnet (Identifikation,
inverses Problem).
Auf geeigneter Modellierung und numerischer nichtlinearer Ausgleichsrechnung
beruhende Verfahren zur indirekten Vermessung kinematischer Parameter
sind mit dem Industriepartner in den Vorarbeiten
zum laufenden Projekt bereits entwickelt und implementiert worden
[Mü].
Die Bestimmung dynamischer Parameter ist jedoch problematischer.
Zur direkten Vermessung dynamischer Parameter,
wie den Massenmittelpunkten und den Trägheitstensoren,
ist die Zerlegung des Roboters und experimentelle Vermessung
jedes einzelnen Teilkörpers mit relativ aufwendigen
Meßapparaturen notwendig [Tü].
Für einen industriellen Einsatz ist es jedoch wünschenswert,
die fehlenden (oder nicht ausreichend genau bekannten) Daten
des Roboters möglichst am Arbeitsplatz
und ohne die Notwendigkeit einer Zerlegung des gesamten Roboters
bestimmen zu können.
Zur Identifikation dynamischer Parameter durch indirekte Vermessung
werden geeignete Testbahnen mit dem Roboter gefahren.
Die unbekannten Modellparameter werden dann so angepaßt,
daß die computersimulierten Bahnen möglichst gut mit
den gemessenen Bahnverläufen übereinstimmen.
Ein erster Ansatz hierzu nützt aus, daß die zu bestimmenden
Trägheitsparameter linear in den Elementen der Massenmatrix M
in Gleichung (1) auftreten.
Wenn man nun annimmt, daß die Steuergröße 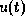 (input)
sowie alle Zustandsgrößen
(input)
sowie alle Zustandsgrößen  ,
, 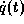 ,
,  (output) für eine Anzahl von Meßzeitpunkten
(output) für eine Anzahl von Meßzeitpunkten 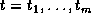 gemessen werden können, so erhält man damit aus
Gleichung (1) ein überbestimmtes lineares
Gleichungssystem für die unbekannten Trägheitsparameter [Hö].
Mit akzeptablem Aufwand können in der Praxis jedoch
weder die zweiten noch die ersten Ableitungen von
gemessen werden können, so erhält man damit aus
Gleichung (1) ein überbestimmtes lineares
Gleichungssystem für die unbekannten Trägheitsparameter [Hö].
Mit akzeptablem Aufwand können in der Praxis jedoch
weder die zweiten noch die ersten Ableitungen von 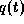 gemessen werden.
Daher müssen als Ersatz
,,künstliche`` Meßwerte für die Ableitungen
von einer Reihe von
Meßwerten
gemessen werden.
Daher müssen als Ersatz
,,künstliche`` Meßwerte für die Ableitungen
von einer Reihe von
Meßwerten  ,
, 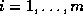 bestimmt werden,
beispielsweise durch Differenzenapproximationen erster und zweiter
Ordnung. Zusätzliche Schwierigkeiten werden dadurch
verursacht, daß die Messungen
bestimmt werden,
beispielsweise durch Differenzenapproximationen erster und zweiter
Ordnung. Zusätzliche Schwierigkeiten werden dadurch
verursacht, daß die Messungen 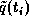 mit Meßfehlern behaftet sind [Hö].
mit Meßfehlern behaftet sind [Hö].
Andererseits können konsistente Werte für 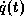 und
und  auch allein aus Messungen von
auch allein aus Messungen von 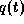 und mit Hilfe numerischer Integration
der Differentialgleichungen (1) berechnet werden.
Die Trägheitsparameter erhält man dann als Lösung eines
nichtlinearen beschränkten Ausgleichsproblems der Form:
und mit Hilfe numerischer Integration
der Differentialgleichungen (1) berechnet werden.
Die Trägheitsparameter erhält man dann als Lösung eines
nichtlinearen beschränkten Ausgleichsproblems der Form:
Man minimiere  hinsichtlich der unbekannten Parameter c und den
(unbekannten) Anfangswerten
hinsichtlich der unbekannten Parameter c und den
(unbekannten) Anfangswerten 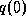 ,
, 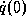

D.h. in Gleichung (3)
ist 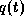 die (numerische) Lösung der
von den unbekannten Parametern c abhängenden Differentialgleichungen,
die das dynamische Verhalten des Roboters beschreiben,
mit optional vorgegebenen Anfangs- oder Endwerten
(Gleichung (5)).
Die numerische Lösung der resultierenden gleichungsbeschränkten
nichtlinearen Ausgleichsprobleme erfolgt
mit verallgemeinerten Gauß-Newton Verfahren
oder angepaßten Verfahren
der Sequentiellen Quadratischen Programmierung (SQP)
[BoEiSchl], [GiMuSaWr], [He].
Dazu ist eine effiziente und zuverlässige Berechnung der
Gradienten
die (numerische) Lösung der
von den unbekannten Parametern c abhängenden Differentialgleichungen,
die das dynamische Verhalten des Roboters beschreiben,
mit optional vorgegebenen Anfangs- oder Endwerten
(Gleichung (5)).
Die numerische Lösung der resultierenden gleichungsbeschränkten
nichtlinearen Ausgleichsprobleme erfolgt
mit verallgemeinerten Gauß-Newton Verfahren
oder angepaßten Verfahren
der Sequentiellen Quadratischen Programmierung (SQP)
[BoEiSchl], [GiMuSaWr], [He].
Dazu ist eine effiziente und zuverlässige Berechnung der
Gradienten 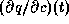 ,
,  erforderlich.
Mehrere Ansätze zur Gradientenberechnung
wurden entwickelt,
implementiert und verglichen [BuHiKi], [He].
erforderlich.
Mehrere Ansätze zur Gradientenberechnung
wurden entwickelt,
implementiert und verglichen [BuHiKi], [He].
Bemerkungen:
Es kann Trägheitsparameter geben,
die konstruktionsbedingt durch indirekte Vermessung nicht bestimmt
werden können (z.B. die Trägheitsmomente bzgl. der
horizontalen Rotationsachsen
im Basisgelenk 1 von Abb. 3).
Andere Parameter wiederum sind möglicherweise nur bis auf einen
gemeinsamen homogenisierenden Faktor eindeutig bestimmbar.
Beispiel:
In Abb.4 ist ein Vergleich zwischen
Computersimulation und Experiment für die im nächsten
Abschnitt beschriebene verbrauchsminimale Bahn
aus Abb. 6
für einen Roboter vom Typ Manutec r3 wiedergegeben.
Beim Basisgelenk gibt es keinen sichtbaren Unterschied
zwischen dem berechneten und experimentellen
Verlauf des Gelenkwinkels 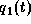 .
Die Unterschiede zwischen der berechneten und tatsächlich
benötigten Steuerung
.
Die Unterschiede zwischen der berechneten und tatsächlich
benötigten Steuerung  sind im Mittelteil
der Bewegung auf die im Simulationsmodell [OtTü]
nicht berücksichtigte Gleitreibung
und am Anfang und am Ende der Bewegung zusätzlich
auf Elastizitäten in den Getrieben zurückzuführen.
Zur Verbesserung des Modells werden die drei Koeffizienten
sind im Mittelteil
der Bewegung auf die im Simulationsmodell [OtTü]
nicht berücksichtigte Gleitreibung
und am Anfang und am Ende der Bewegung zusätzlich
auf Elastizitäten in den Getrieben zurückzuführen.
Zur Verbesserung des Modells werden die drei Koeffizienten
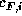 , i=1,2,3 eines Coulomb-Reibungsansatzes
, i=1,2,3 eines Coulomb-Reibungsansatzes

durch Parameteridentifikation aus 400 Messungen berechnet.
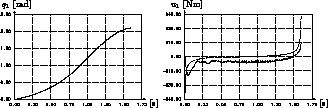
Figure: Verlauf von Winkel  und Steuerung
und Steuerung 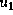 des Basisgelenks
für die verbrauchsminimale Steuerung (Abb. 6)
in Simulation (--
des Basisgelenks
für die verbrauchsminimale Steuerung (Abb. 6)
in Simulation (-- --)
und Experiment (------).
--)
und Experiment (------).



Next: Bahnoptimierung
Up: Beschreibung der zu
Previous: Modellierung
Oskar von Stryk
Thu Jan 23 09:41:06 MET 1997
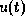 (input)
sowie alle Zustandsgrößen
(input)
sowie alle Zustandsgrößen  ,
, 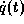 ,
,  (output) für eine Anzahl von Meßzeitpunkten
(output) für eine Anzahl von Meßzeitpunkten 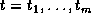 gemessen werden können, so erhält man damit aus
Gleichung (1) ein überbestimmtes lineares
Gleichungssystem für die unbekannten Trägheitsparameter [Hö].
Mit akzeptablem Aufwand können in der Praxis jedoch
weder die zweiten noch die ersten Ableitungen von
gemessen werden können, so erhält man damit aus
Gleichung (1) ein überbestimmtes lineares
Gleichungssystem für die unbekannten Trägheitsparameter [Hö].
Mit akzeptablem Aufwand können in der Praxis jedoch
weder die zweiten noch die ersten Ableitungen von 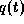 gemessen werden.
Daher müssen als Ersatz
,,künstliche`` Meßwerte für die Ableitungen
von einer Reihe von
Meßwerten
gemessen werden.
Daher müssen als Ersatz
,,künstliche`` Meßwerte für die Ableitungen
von einer Reihe von
Meßwerten  ,
, 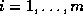 bestimmt werden,
beispielsweise durch Differenzenapproximationen erster und zweiter
Ordnung. Zusätzliche Schwierigkeiten werden dadurch
verursacht, daß die Messungen
bestimmt werden,
beispielsweise durch Differenzenapproximationen erster und zweiter
Ordnung. Zusätzliche Schwierigkeiten werden dadurch
verursacht, daß die Messungen 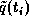 mit Meßfehlern behaftet sind [Hö].
mit Meßfehlern behaftet sind [Hö].
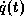 und
und  auch allein aus Messungen von
auch allein aus Messungen von 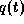 und mit Hilfe numerischer Integration
der Differentialgleichungen (
und mit Hilfe numerischer Integration
der Differentialgleichungen ( hinsichtlich der unbekannten Parameter c und den
(unbekannten) Anfangswerten
hinsichtlich der unbekannten Parameter c und den
(unbekannten) Anfangswerten 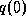 ,
, 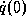

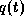 die (numerische) Lösung der
von den unbekannten Parametern c abhängenden Differentialgleichungen,
die das dynamische Verhalten des Roboters beschreiben,
mit optional vorgegebenen Anfangs- oder Endwerten
(Gleichung (
die (numerische) Lösung der
von den unbekannten Parametern c abhängenden Differentialgleichungen,
die das dynamische Verhalten des Roboters beschreiben,
mit optional vorgegebenen Anfangs- oder Endwerten
(Gleichung (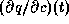 ,
,  erforderlich.
Mehrere Ansätze zur Gradientenberechnung
wurden entwickelt,
implementiert und verglichen [
erforderlich.
Mehrere Ansätze zur Gradientenberechnung
wurden entwickelt,
implementiert und verglichen [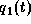 .
Die Unterschiede zwischen der berechneten und tatsächlich
benötigten Steuerung
.
Die Unterschiede zwischen der berechneten und tatsächlich
benötigten Steuerung  sind im Mittelteil
der Bewegung auf die im Simulationsmodell [
sind im Mittelteil
der Bewegung auf die im Simulationsmodell [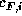 , i=1,2,3 eines Coulomb-Reibungsansatzes
, i=1,2,3 eines Coulomb-Reibungsansatzes


 und Steuerung
und Steuerung 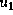 des Basisgelenks
für die verbrauchsminimale Steuerung (Abb.
des Basisgelenks
für die verbrauchsminimale Steuerung (Abb.  --)
und Experiment (------).
--)
und Experiment (------).