


Next: Section NAMEN
Up: Input File of PAREST
Previous: Input File of PAREST
This section contains the description of the dimensions of the problem and of
optional parameters of the optimization method.
They are set by assigning values to the following variable names:

The selection between parameter identification and optimal control
problems is done by setting

Free or prescribed initial and final time are set by using the statements
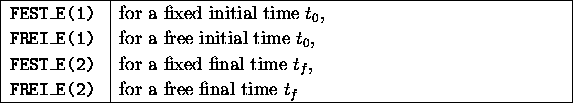
in this section of the input file.
Three different methods can be selected for the numerical
integration of the dynamical equations (1)
- DASSL: the initial-value problem solver for
differential-algebraic equations of [13]
(backward difference formulas)
with the extensions of [1]
for a numerical sensitivity analysis.
- DOPRI8: the initial-value problem solver for ordinary differential
equations of [10]
(8th order extrapolation method) with the extensions
of [6]
for a numerical sensitivity analysis.
- RKF4: an initial-value problem solver for ordinary differential equations
(4th order Runge/Kutta method) with the extensions
of [6]
for a numerical sensitivity analysis.

As a rule of thumb, the tolerances for integration should be
less or equal one tenth of the tolerances for optimization (see below),
for example,
RTOL 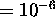 and OPTTOL
and OPTTOL 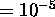 (see description below).
(see description below).
Three iterative methods for optimization are available:
- NLSCON (Nowak, Weimann
[11], [12]):
a generalized Gauß-Newton method for nonlinear least
squares problems subject to nonlinear equality constraints
[8]
(NLSCON
can only be used for parameter identification problems
and not for optimal control problems), - NPSOL (Gill, Murray, Saunders, Wright
[9]):
a Sequential Quadratic Programming (SQP) method for
general nonlinearly constrained optimization problems
[14]
(NPSOL is the
only possible selection for optimal control problems.
It may also be selected for parameter identification problems
but will usually be less efficient than NLSSOL
or NLSCON), - NLSSOL (Gill, Murray, Saunders, Wright
[9]):
an SQP-method for nonlinear least squares problems
subject to general nonlinear equality and inequality constraints
(NLSSOL
can only be used for parameter identification problems
and not for optimal control problems).





Next: Section NAMEN
Up: Input File of PAREST
Previous: Input File of PAREST
Oskar von Stryk
Tue Feb 1 13:50:42 CET 2000



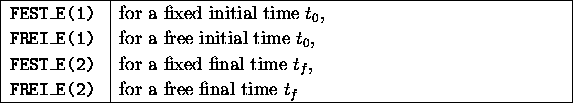

![]() and OPTTOL
and OPTTOL ![]() (see description below).
(see description below).

