Dynamic model

The dynamic model is described by a system of differential-algebraic equations of index 1 in semi-explicit form:

 

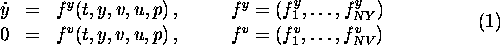
Notation

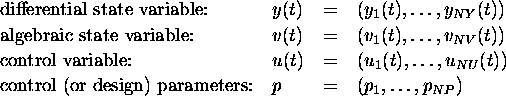
(In the case of a dynamical system of only ordinary differential equations NV is zero.)

Further problem dependent functions are:

• boundary conditions (including initial and final conditions of the state variables) defined by

   

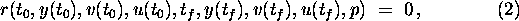
  where ,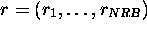

• (nonlinear) inequality constraints on the control and state variables

   

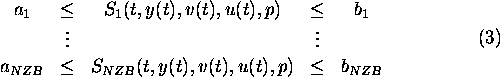
  (Constraints of this kind usually appear more often in optimal control than in parameter estimation problems.)

• (general) functions of the state (and control) variables

   

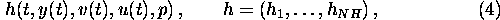
  which may be used for two different purposes:

  • In parameter identification problems the state variables y(t) and v(t) often cannot be measured directly. But functions h of them have been measured in an experiment. The relation between the measured quantities and the state variables is given by the function h(t,y,v,u,p).
  • PGRAPH also generates graphical output of the functions 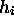. Therefore any functions 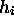of the state and control variables might be used in addition for the purpose of monitoring properties of the computed trajectories (for example, phase diagrams as the altitude/velocity diagram in optimal control problems from flight mechanics, or violations of algebraic index-2- or index-3-constraints if index reduction has been applied to a problem with a system of differential-algebraic equations of a higher index (as in the pendulum problem described in Section 5.1)).

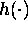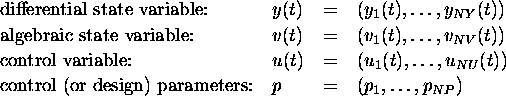
  The components of the functions do only enter the optimization program PAREST if they are required in a parameter estimation problem. Otherwise they will only be used for plotting by PGRAPH.