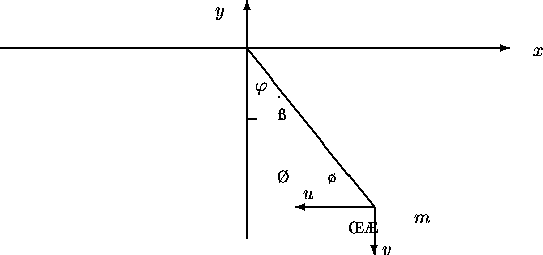
Consider a pendulum of length l and mass m which is fixed at the origin of a coordinate system and moves in the x-y plane.
We consider the formulation of the dynamics of motion
as a system of differential-algebraic equations.
If 
denotes the Lagrangian multiplier
and g the gravitational constant
then the Lagrangian is
Now substituting 
, 
for the velocities
and applying index reduction techniques,
the equations of motions read as a system of differential-algebraic
equations of index 1
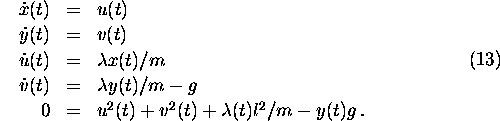
Whereas the two additional entry conditions to be satisfied at 
due to the index reduction are
Now the dynamic model has the dimensions
NY = DIMY = 4, NV = DIMV = 1, NU = DIMU = 0, NP = NPAR = 1, NRB = NRB = 2, NZB = NZB = 0.
We assume that the gravitational constant g is unknown
and has to be identified by using the results of an experiment:
The pendulum moves for two seconds.
After every 0.2 seconds the values of x(t), y(t),
and 
are measured (but the values of
the velocities u(t), v(t) are not).
This gives 11 times 
,..., 
of measurements
and 33 measurement values in total.
It is assumed that the measurements are not fully precise
but with measurement errors of standard deviations of
and 
.
These weights will be used as weights 
in the nonlinear least squares objective
of Equation (5).
A multiple shooting node is selected at every time of measurement.
As initial estimates of the state variables x(t), y(t) and
at the multiple shooting nodes we simply use the given measurements.
Initial estimates of the velocities u(t), v(t)
can be computed by local interpolation of the measurements
of x(t), y(t).
As initial estimate of the parameter g
we use 
.
The ''true'' value of g is 
.